<< Click to Display Table of Contents >> Navigation:  Pavement Concepts > Stress

The cncPAVE program calculates the maximum tensile stress at a joint or crack. The calculation is based on a regression equation. For more accurate calculations and specialized applications, a finite element program should be used to calculate stress.

 

The maximum stress in a concrete slab that is placed on an elastic support can be calculated using different equations, or theories. The most well-known method is that of Westergaard (1). Since the publication of his equations several other methods have been developed (2).

Stress in a pavement is based on the following general relationship:

 

 

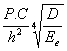
where

 

C      factor that mainly depends on slab configuration and load transfer at joints

P      magnitude of traffic loading

D      slab stiffness

Ee     slab support stiffness

h       slab thickness.

 

The different parameters in the above equation can further be defined as functions of other parameters:

 

•The factor C depends on load transfer at joints or cracks, through the mechanism of aggregate interlock and is therefore primarily a function of crack width (Dx), and aggregate shape and size (Agg). If dowel bars and steel reinforcement bars are used for load transfer, C is also a function of steel diameter (dia) and the concrete stiffness or bearing capacity of the concrete around the steel. These properties change with time.

•Magnitude of traffic loading P is a function of contact pressure (p), wheel load and speed of traffic.

•Slab stiffness D is a combination of slab thickness and concrete stiffness (E). The latter depends on the characteristics of the concrete mix and its different components as well as construction methods, curing and environmental influences.

•Support stiffness Ee is dependent on the stiffness values as well as thicknesses of the different supporting layers. Slab support can change because of a change in moisture content, curling and other external factors. Voids can also develop as a result of subgrade settlement, erosion and pumping of the support layers and reduce slab support.