<< Click to Display Table of Contents >> Navigation:  Statistical Concepts > Triangular Probability Distribution

Due to uncertainty, the designer may find it difficult to determine appropriate values for input variables. Many designers realize the uncertainty inherent to input figures and try to avoid the use of the so-called single point estimates. Instead, they use their experience and indicate a range of reasonable practical values.

 

In the cncPAVE program triangular probability distribution has been used to express the stochastic nature of input variables. Triangular distribution is defined by three parameters, namely

 

•minimum practical value,

•the best estimate, and

•maximum practical value.

 

Triangular distribution (see the sketch below) has been chosen in preference to the Normal, Lognormal, Gumbel or Weibull probability distributions, because the determination of its parameters appeals to intuition, and is conducive to a direct application of the designer's experience.

 

 

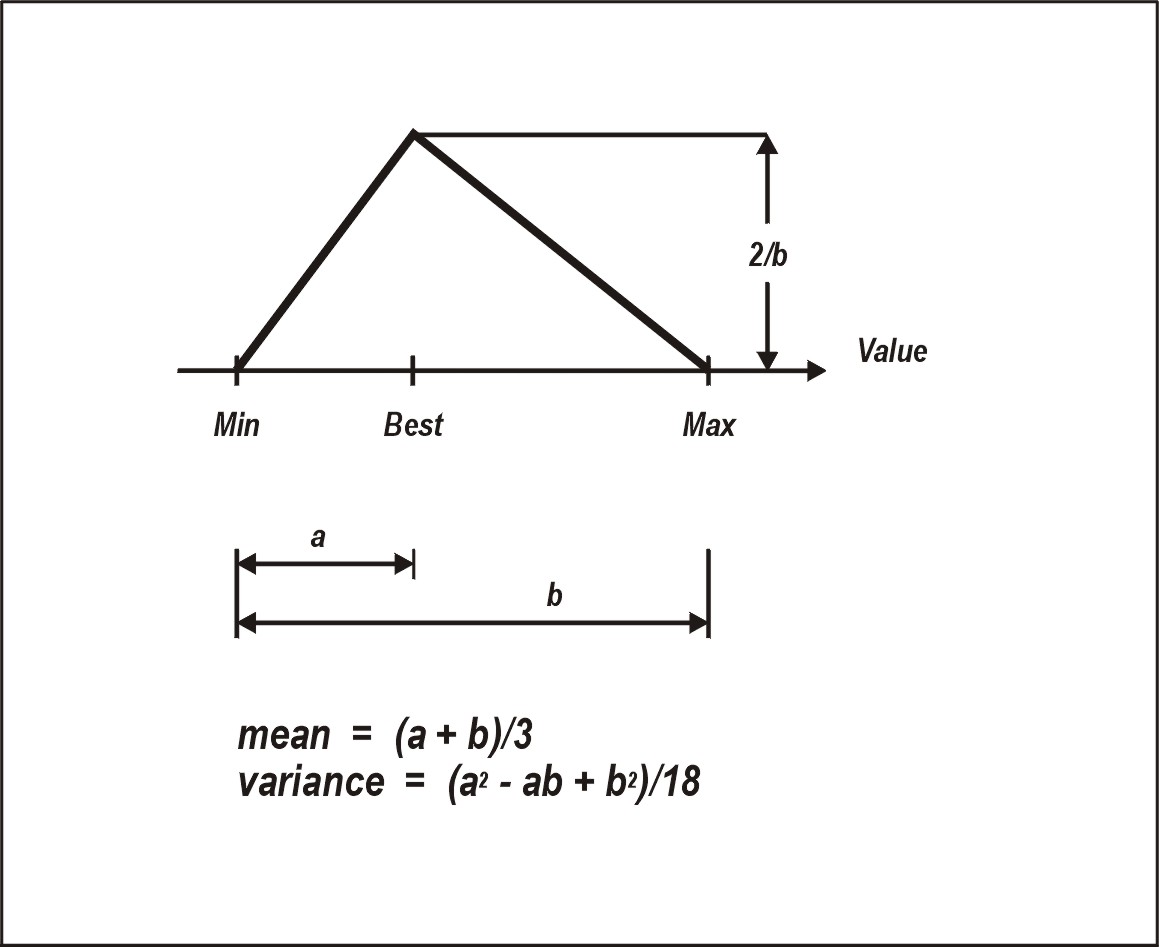
The selection of parameters has certain consequences. A conservative, uninformed, or unsure designer tends to specify triangular distributions with low minimum, and high maximum, practical values. This, however, results in 'fat' (i.e. very dispersed) distributions of decision variables, with wide confidence intervals. A wide confidence interval of a decision variable implies a high probability of that variable exceeding an acceptable value. To bring the figure down, a stronger - and more expensive - pavement will have to be employed. The extra cost of such pavement should then be viewed as the cost of the designer's inexperience and his or her imperfect knowledge of input.